Subject

I was previously a PhD student in the Jacques-Louis Lions laboratory in Jussieu, in the Emmanuel Trélat and Thomas Haberkorn direction. Subject: Obtaining optimal trajectories using the invariant manifolds of Lagrange points from the 3-body system.

This thesis was defended on the 19th of octobre 2016, the jury was composed by Jean-Baptiste Caillau, Pascal Frey, Richard Épenoy, Emmanuel Trélat, Thomas Haberkorn and Max Cerf.

Thesis Manuscript

Manuscript: these.pdf.
Slides of the defense: soutenance.pdf.

Description générale [French]

Sur cette page, un bref aperçu de la problématique. Par souci de concision, il y a des raccourcis, et donc des imprécisions.

But

On cherche à amener un engin spatial d’un ensemble $M_1$ du système solaire à un ensemble $M_2$.

Dans le système solaire, notre engin est soumis à la dynamique
suivante :

\[\ddot{q}(t) = -\mu_\mathrm{SUN} \frac{q(t)-q_\mathrm{SUN}(t)}{\|q(t)-q_\mathrm{SUN}(t)\|^3}+\sum_{i=1}^9 \mu_i \left( \frac{q(t)-q_i(t)}{\|q(t)-q_i(t)\|^3} \right) + \frac{T(t)}{m(t)},\]

avec $q$ la position, $T$ la poussée et $m$ la masse de l’engin.

Différents types de poussée

Suivant le cas, on considère deux types de poussée, une poussée impulsionnelle modélisée par un changement instantanée de vitesse (noté $\Delta V$), et une poussée faible i.e. un contrôle sur la vitesse (noté ci-dessus $T(t)$).

Approximation pour résoudre le problème

Pour résoudre le problème trop complexe dans sa forme de base, on a recours à une approximation : on considère l’attraction gravitationnelle la «plus importante» localement. En première approximation, on utilise l’influence d’un seul corps et on construit les trajectoires par jonction d’orbites képlériennes. Dans ce projet,nous utilisons l’influence de deux corps sur le satellite et les trajectoires sont construites en couplant plusieurs de ces problèmes à trois corps.

Propriétés du problème à trois corps

Dynamique

La dynamique du problème à 3 corps est la suivante pour l’état :

\[X=\left(x,y,z,\dot{x},\dot{y},\dot{z}\right)^T=\left(x_1,x_2,x_3,x_4,x_5,x_6\right)^T,\]

\[ \left\{% \begin{aligned} \dot{x_1}&=x_4\\ \dot{x_2}&=x_5\\ \dot{x_3}&=x_6\\ \dot{x_4}&=x_1+2x_5-(1-\mu)\frac{x_1-x_1^0}{r_1^3}-\mu\frac{x_1-x_2^0}{r_2^3}\\ \dot{x_5}&=x_2-2x_4-(1-\mu)\frac{x_2}{r_1^3}-\mu\frac{x_2}{r_2^3}\\ \dot{x_6}&=-(1-\mu)\frac{x_3}{r_1^3}-\mu\frac{x_3}{r_2^3} \end{aligned} \right.\Leftrightarrow \left\{% \begin{aligned} \dot{x_1}&=x_4=f_1(X)\\ \dot{x_2}&=x_5=f_2(X)\\ \dot{x_3}&=x_6=f_3(X)\\ \dot{x_4}&=2x_5-\frac{\partial U}{{\partial x_1}}=f_4(X)\\ \dot{x_5}&=-2x_4-\frac{\partial U}{\partial {x_2}}=f_5(X)\\ \dot{x_6}&=-\frac{\partial U}{\partial {x_3}}=f_6(X) \end{aligned} \right.
\]
où $U$ est le potentiel :
\[
U(x_1,x_2,x_3)=-\frac{1}{2}\left(x_1^2+x_2^2\right)-\frac{1-\mu}{r_1}-\frac{\mu}{r_2}-\frac{1}{2}\mu\left(1-\mu\right),
\]
et
\[\mu=\frac{m_{2}}{m_{1}+m_{2}}.\]

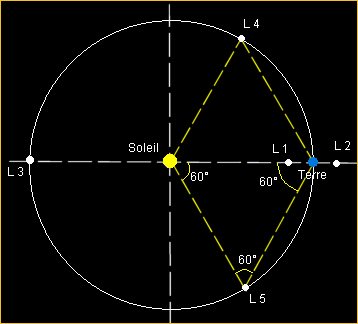
Points de Lagrange

Lagrange puis Euler ont montré l’existence de 5 points d’équilibre notés $L_i$, $i\in\{1,\dots,5\}$.

Illustration points de Lagrange.

Stabilité des points de Lagrange

L’étude de la stabilité des points de Lagrange se fait par linéarisation du système. Il faut distinguer le cas planaire du cas spatial. Toujours est-il qu’on arrive aux conclusions suivantes

Dans tous les cas, les point $L_1$, $L_2$ et $L_3$ sont instables.
Il faut une études spéciale pour les points équilatéraux. Il arrive que ceux-ci soit stables. L’image ci-dessous montre tout un tas de débris près des points $L_4$ et $L_5$ du système Soleil-Jupiter, qui les rendent inutilisables pour le transfert de satellite.

Illustration des débris appelés grecques et troyens sur l'orbite de Jupiter.

Orbites périodiques

Le théorème de Lyapunov-Poincaré appliqué au points d’équilibre du problème des trois corps nous assure l’existence d’orbites périodiques autour de ces points. Plus précisément :

dans le cas planaire, on a une famille d’orbites périodiques à un paramètre, appelées orbites de Lyapunov;
dans le cas spatial, on a une famille d’orbites à deux paramètres. Ci-dessous, la représentation de deux types d’orbites, celles homéomorphes à un cercle qu’on appelle orbites de Halo, et un autre type d’orbites en huit.

Variétés invariantes

De ces orbites périodiques, sont issues des variétés invariantes. La définition de ces variétés est la suivante :

La variété stable (resp. instable) d’une orbite périodique est le sous-ensemble de l’espace des phases formé par tous les points dont la demi-orbite future (resp. passée) converge vers l’orbite périodique.

Les variétés invariantes issues d'orbites périodique autour des points $L_1$ et $L_2$.

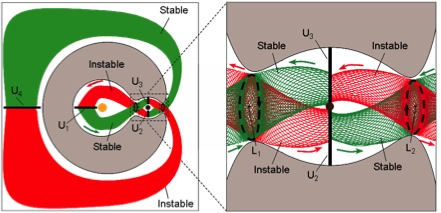
Sur l’image ci-dessus, on voit les différentes variétés invariantes issues de deux orbites périodiques autour des points $L_1$ et $L_2$.

Ces variétés sont des séparatrices du système dynamique. Par conséquent, elles peuvent être vues comme des sortes de courants gravitationnels et donc elle peuvent aider à construire des missions en nous permettant d’économiser du carburant.

Construction de missions

Ces courants gravitationnels se révèlent très utiles pour construire des missions à faible consommation. À l’image des courants marins, on essaie au maximum de s’en servir.

Par impulsion

Lorsqu’on utilise des poussées fortes sur nos satellites, modélisées par un changement instantané de vitesse $\Delta V$. L’idée est alors de chercher des intersections des courants gravitationnels en espace et de passer de l’un à l’autre avec un changement instantanné de vitesse.

La vue d’artiste suivante permet de visualiser un peu l’idée de telles missions. En faisant une cartographie des
différents tubes des différents problèmes des trois corps du système solaire, on peut construire un chemin à coût de consommation très faible, passant d’un tube à l’autre avec une impulsion.

Ensemble de tubes qui permettent de construire une mission.

En poussée faible

En poussée faible, cette technique n’est plus utilisable. C’est sur ce problème que nous travaillons actuellement. En utilisant le principe du maximum de Pontryagin pour résoudre un problème de contrôle optimal formulé pour réaliser un tel transfert, on cherche par une méthode de tir (méthode indirecte), à trouver le zéro d’une fonction. L’idée est alors d’utiliser l’analyse géométrique de la dynamique couplée à l’utilisation de méthodes homotopiques pour initialiser la méthode de Newton.

Financement

Ma thèse est financée par Airbus Defence and Space en thèse CIFRE en collaboration avec le LJLL-UPMC et le MAPMO d’Orléans. Les directeurs de thèse sont Philippe Augros (Airbus), Thomas Haberkorn (Orléans) et Emmanuel Trélat (UPMC Paris).