Jouer au billard, mais de façon dissipative
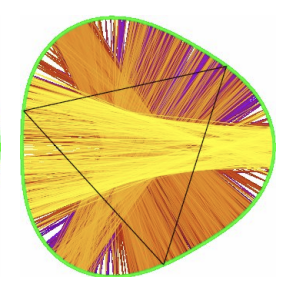
Un billard mathématique est la donnée d’une région fermée du plan (la table) à l’intérieur de laquelle un point sans masse (la boule) se déplace de façon rectiligne jusqu’à rencontrer le bord. Quand la boule rebondit, dans la version usuelle (conservative) du billard, son angle d’incidence est égal à l’angle de réflexion : après le rebond, elle continue en ligne droite jusqu’à rencontrer à nouveau le bord, et ainsi de suite.
Une classe largement étudiée de billards sont les billards de Birkhoff, pour lesquels la table est une région convexe suffisamment régulière. Que se passe-t-il à présent si on essaie de tenir compte de phénomènes de dissipation lors des collisions de la boule avec le bord de la table ? On introduit de la dissipation en modifiant la loi de réflexion usuelle de la façon suivante : quand la boule tape le bord du billard, la direction du vecteur vitesse est progressivement rapprochée de celle orthogonale au bord, au fur et à mesure des rebonds. Quels comportements dynamiques en temps long vont-ils alors apparaître ?
Dans ces billards dissipatifs, il existe un ensemble invariant satisfaisant certaines propriétés de minimalité, appelé attracteur de Birkhoff, qui garde l’essentiel de l’information sur le comportement en temps long des orbites : en particulier, la dynamique restreinte à cet ensemble permet de dire si la dynamique est complexe ou pas. Olga Bernardi (Università degli Studi di Padova), Anna Florio (CEREMADE) et Martin Leguil (École Polytechnique) ont montré que, pour un billard convexe générique où la dissipation est suffisamment faible, l’attracteur de Birkhoff correspondant est compliqué, à la fois du point de vue dynamique (il présente des comportements chaotiques, notamment, une forte sensibilité aux conditions initiales) et du point de vue topologique (il ne peut pas être décomposé simplement : par exemple, il ne peut pas s'écrire comme l'union de deux ensembles compacts connexes non triviaux).
Contact : florio@ceremade.dauphine.fr
L'énergie des molécules est-elle une fonction convexe ?
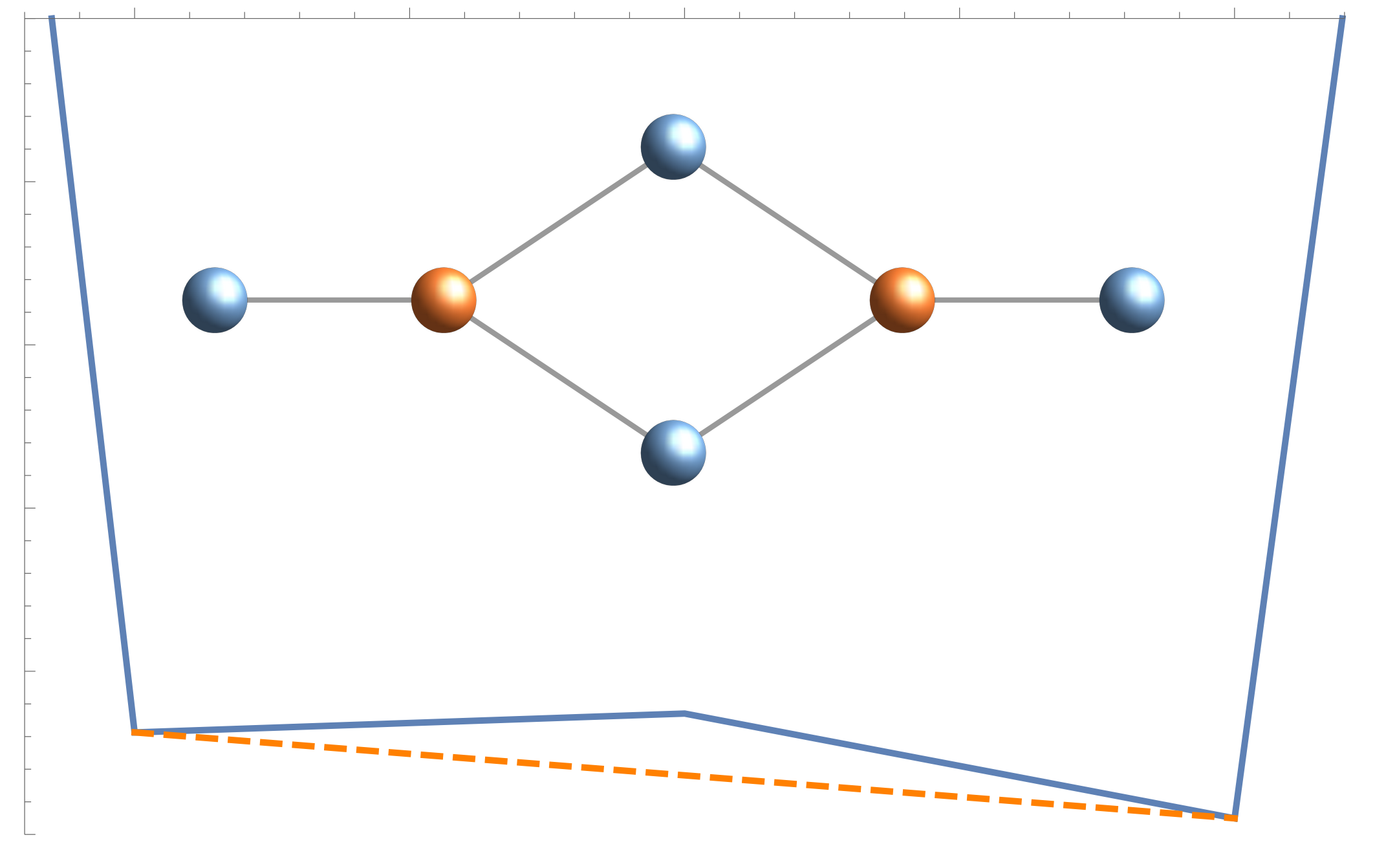
Prenons un atome ou une molécule et tentons d’enlever ses électrons un par un. On s’attend à attraper à chaque fois l’électron qui est le plus faiblement lié au système, et donc que la difficulté augmente au cours du processus. C'est bien ce qu'on observe expérimentalement. Si on trace l'énergie d'un atome en fonction du nombre d'électrons qu'il contient, on obtient une fonction décroissante et convexe (linéaire par morceaux). La convexité signifie précisément qu'enlever des électrons coûte de plus en plus cher énergétiquement, en valeur absolue.
Montrer la convexité de cette courbe d'énergie lorsque les électrons sont décrits par l'équation de Schrödinger est un problème mathématique célèbre qui a été formulé dans les années 1980. Ce problème est resté bloqué pendant plus de 40 ans.
Dans un article publié en novembre 2024 dans le Journal of Physical Chemistry A, Simone Di Marino (Gênes, Italie), Mathieu Lewin (Ceremade, Dauphine-PSL) et Luca Nenna (Paris-Saclay) ont trouvé le premier exemple d'une molécule comprenant 6 atomes et 4 électrons, pour laquelle il est plus facile d'enlever deux électrons que d'en enlever un seul. Les noyaux considérés ont des charges fractionnaires, alors que les noyaux réels ont une charge entière. Ce contre-exemple jette néanmoins un fort doute sur la validité de la conjecture en toute généralité.
Ce travail est basé sur des techniques de transport optimal qui avaient été développées dans un précédent article mathématique de 2022, en apparence sans aucun rapport avec l'ionisation des molécules. Ce dernier article va paraître dans Archive for Rational Mechanics and Analysis.
Contact : lewin@ceremade.dauphine.fr
Décomposition de Karhunen-Loève et processus de Hawkes
La décomposition de Karhunen-Loève est un résultat central dans l'étude des processus stochastiques. Elle permet de caractériser l'écart d'un processus $(X_{t})_{t\in [0,1]}$ à sa moyenne, qui peut s'écrire de la manière suivante : $$(1)\quad X_{t} -\mathbb E[X_t] =\sum_{j\geq 1}\sqrt\lambda_j\xi_j\psi_j(t),$$
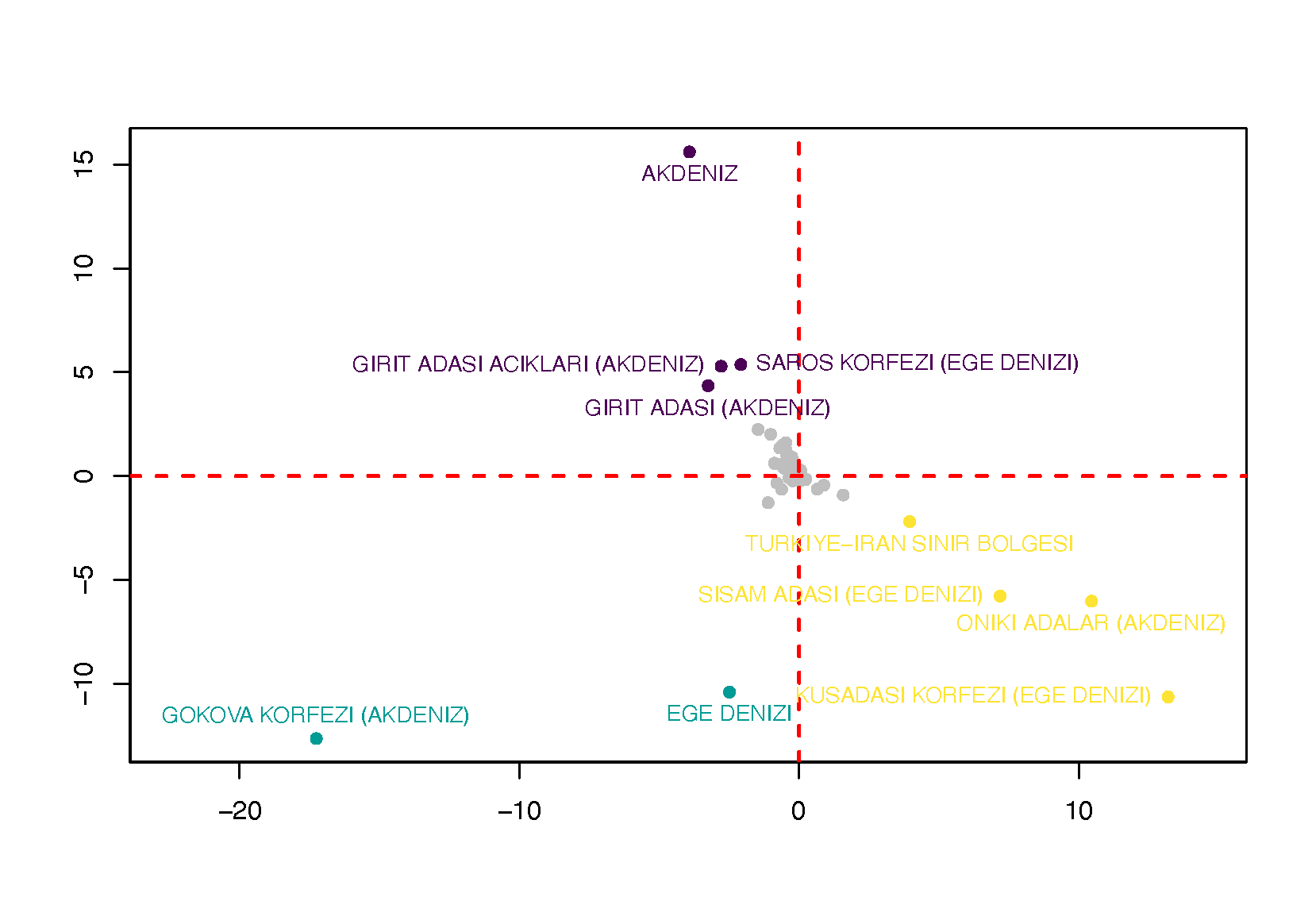
où $(\lambda_j)_{j\geq 1}$ est une suite sommable de nombres positifs, $(\xi_j)_{j\geq 1}$ est une suite de variables aléatoires non-corrélées, appelées scores, et $(\psi_j)_{j\geq 1}$ est une base orthonormée de $\mathbb L^2([0,1])$ qui s'adapte au processus afin de fournir la meilleure base possible pour sa décomposition (au sens de l'erreur quadratique moyenne). La décomposition de Karhunen-Loève joue donc un role clé en statistique en donnant par exemple tout son sens à l'Analyse en Composantes Principales pour données fonctionnelles. En particulier, c'est en s'appuyant sur les scores que nous obtenons une visualisation aisée ou le clustering des données.
La généralisation de ce type de résultat aux processus ponctuels a été proposée par Victor Panaretos (EPFL), Franck Picard (ENS Lyon), Vincent Rivoirard (Ceremade) et Angelina Roche (Ceremade). Plus précisément, si $\Pi$ désigne la mesure de comptage associée à un processus ponctuel sur $[0,1]$ telle que $\mathbb E[\Pi^2[0,1]]<+\infty,$ alors $\Pi$ peut s'écrire, pour tout borélien $A$, $$\Pi(A)-\mathbb E[\Pi(A)] = \sum_{j\geq 1}\sqrt\lambda_j\xi_j\mu_j(A),$$ où cette fois $(\mu_j)_{j\geq 1}$ désigne une suite de mesures signées, les autres termes de la somme ayant la même signification que dans $(1)$. Par ailleurs les fonctions $t\longmapsto \mu_j([0,t])$ constituent une base orthonormée de $\mathbb L^2([0,1])$.
Il est alors naturel d'illustrer ces résultats sur les processus ponctuels les plus classiques, comme les processus de Poisson ou les processus de Hawkes. Rappelons que ces derniers permettent de modéliser les événements présentant un comportement auto-excitant comme par exemple les tremblements de terre (voir figure ci-dessus). Ils sont très utilisés en neurosciences, en épidémiologie, en finance ou pour l'analyse des réseaux sociaux. Pour ces exemples de processus, on obtient les valeurs des éléments $(\lambda_j,\mu_j)_{j\geq 1}$ en résolvant le système :
$$ -\lambda y''(t)=w(t)y(t)+\int_0^1 m(s,t)y(s)ds , \quad t\in(0,1)$$ $$y(1) =0,\quad y'(0)=0$$
où les fonctions $w$ et $m$ dépendent des paramètres du processus étudié.
Contacts : Angelina Roche (roche@ceremade.dauphine.fr) et Vincent Rivoirard (rivoirard@ceremade.dauphine.fr),
Panaretos, V., Picard, F., Rivoirard, V. et Roche A. PCA for point processes, work in progress.
Indices topologiques et ondes équatoriales
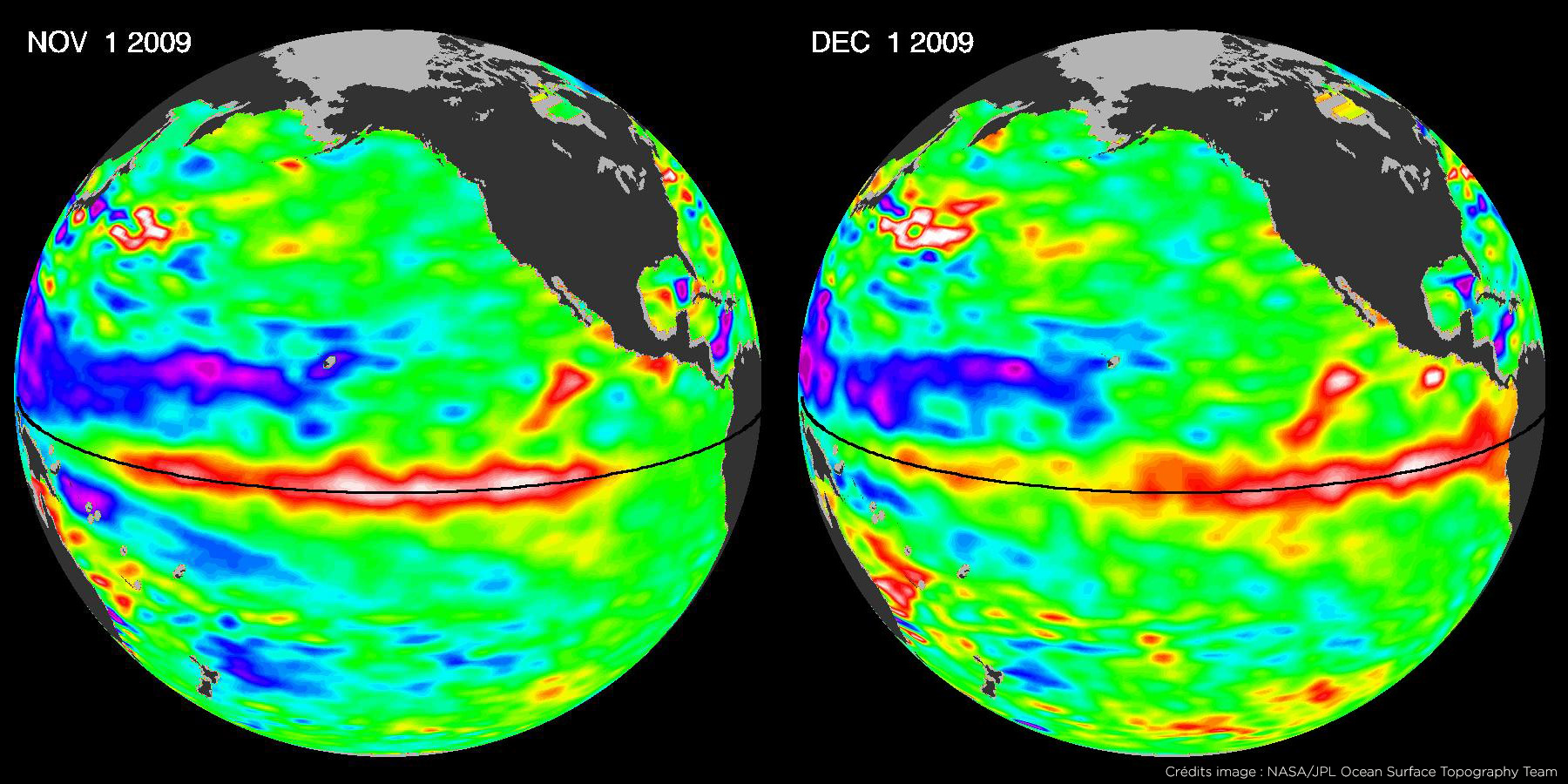
L'onde de Kelvin équatoriale est un phénomène météorologique observé à la surface de l'océan pacifique, qui se propage exclusivement vers l'est sur des milliers de kilomètres tout en restant confinée à l'équateur avec une remarquable stabilité. Cette onde joue un rôle important dans l'apparition du phénomène El Niño. D'autres ondes équatoriales, comme l'onde de Yanai, présentent des propriétés similaires.
La propagation de ces ondes est décrite par un modèle de mécanique des fluides appelé ondes en eau peu profonde (shallow-water). La force de Coriolis, due à la rotation de la Terre, y joue un rôle central : elle change de signe en passant de l'hémisphère nord à l'hémisphère sud et s'annule à l'équateur. Avec Pierre Delplace (ENS Lyon) et Antoine Venaille (ENS Lyon), Clément Tauber (CEREMADE) a montré que ce modèle est formellement analogue à un problème de mécanique quantique pour lequel on peut définir des indices topologiques associés aux ondes équatoriales. La nature topologique de ces ondes, notamment la correspondance bord-volume, permet d'expliquer leur stabilité exceptionnelle, un phénomène bien connu en physique du solide, dans les isolants topologiques et l'effet Hall quantique. Ici, la force de Coriolis joue le rôle du champ magnétique.
Par ailleurs, avec Gian Michele Graf (ETH Zürich) et Hansueli Jud (ETH Zürich), Clément Tauber (CEREMADE) a étudié les propriétés spectrales de l'opérateur associé au modèle et révélé certaines singularités asymptotiques dans le spectre qui donnent un théorème de correspondance bord-volume généralisé, permettant une compréhension plus fine sur la stabilité de ces ondes, notamment leur propagation en présence d'une côte plutôt qu'à l'équateur.
https://doi.org/10.1017/jfm.2019.233
https://doi.org/10.1007/s00220-021-03982-7
Contact : tauber@ceremade.dauphine.fr
Le choix d'études mathématiques par les filles serait-il biaisé?

Le choix d'études mathématiques par les filles serait-il biaisé?
Bien que les filles soient actuellement plus nombreuses que les garçons dans l'enseignement supérieur, elles restent largement sous-représentées dans les domaines d'études liés aux mathématiques, sans aucun signe d'amélioration au cours des dernières décennies.
Pour mieux comprendre quels élèves sont à l'origine de cette sous-représentation, une équipe interdisciplinaire composée de Thomas Breda (ENS), Elyès Jouini (Ceremade) et Clotilde Napp (DRM) a utilisé les données de l'enquête PISA 2012 sur 251 120 élèves de 15 ans dans 61 pays afin d'analyser les intentions éducatives des garçons et des filles en fonction de la distribution des aptitudes aux tests d'évaluation des mathématiques. Ils analysent les pourcentages de garçons et de filles ayant l'intention de poursuivre des études ou des carrières liées aux mathématiques en fonction de la performance en mathématiques.
Tout d'abord, ils montrent que pour les garçons comme pour les filles, il existe une relation positive et linéaire entre la probabilité d'avoir l'intention de poursuivre des études de mathématiques et les performances en mathématiques.
Deuxièmement, cette relation positive est plus forte chez les garçons que chez les filles. En particulier, l'écart entre les sexes dans les intentions des élèves de poursuivre des études ou des carrières liées aux mathématiques est proche de zéro parmi les élèves les moins performants en mathématiques et augmente régulièrement avec la performance en mathématiques.
Troisièmement, en conséquence, l'écart de performance en mathématiques entre les sexes, au détriment des filles, est plus important chez les élèves ayant l'intention de poursuivre des études ou une carrière en mathématiques que dans l'ensemble de la population étudiante.
https://www.nature.com/articles/s41467-023-39079-z
Contact : jouini@ceremade.dauphine.fr
Transport électronique dans le bi-graphène twisté
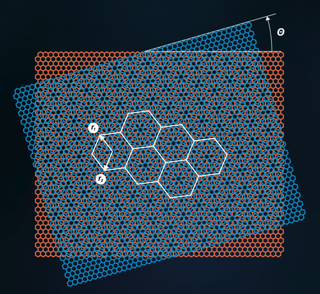
Le graphène est un matériau aux propriétés étonnantes. Pour commencer, il est deux-dimensionnel (c'est une feuille dont l'épaisseur est l'atome), composé d'atomes de carbone qui se répartissent selon un réseau hexagonal. Le "bi-graphène twisté" (TBG) est obtenu en superposant deux feuilles de graphène, l'une sur l'autre, avec un petit angle entre ces feuilles. La superposition des deux réseaux, donne de magnifiques motifs, et possède des propriétés de transport électronique remarquables, comme la superconductivité. Malheureusement, l'étude détaillée du TBG nécessiterait d'étudier des structures avec plusieurs dizaines de milliers d'atomes, ce qui est impossible avec les capacités de calcul actuelles.
Avec Éric Cancès (Ecole des Ponts Paris-Tech) et Louis Garrigue (CY Tech), David Gontier (Ceremade) a proposé une méthode pour réduire l'étude du transport électronique dans le TBG à un nombre très faible de dimensions. Les résultats obtenus avec ce modèle simplifié sont en accord avec les expériences.
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.107.155403
Contact : gontier@ceremade.dauphine.fr
Sur l’accélération d’Anderson-Pulay

Dans de nombreux problèmes (en physique, en chimie, en informatique, en machine learning, etc.), il faut résoudre un problème dit de point fixe: étant donné une fonction $g:\mathbf{R}^n\to\mathbf{R}^n$, trouver $x^\star$ tel que $$x^\star=g(x^\star).$$
La méthode de résolution numérique du point fixe consiste alors à utiliser le schéma itératif suivant:
$$\forall k\in\mathbf{N}, x_{k+1}=g(x_k).$$
À chaque étape, on calcule un résidu : $$r_k=f(x_k)$$ où $f:\mathbf{R}^n\to\mathbf{R}^p$ vérifie $$f(x^\star)=0.$$ Cette fonction de résidu permet en particulier de décider numériquement à quelle étape du schéma itératif on peut s'arrêter.
La résolution de ce problème est souvent trop lente. Dans leur travail de recherche, Maxime Chupin, Mi-Song Dupuy, Guillaume Legendre et Eric Séré se sont intéressé à la classe d'algorithmes d'Anderson-Pulay, permettant d'accélérer la convergence de problèmes de point fixe en utilisant à chaque étape non plus seulement le dernier itéré $x_k$ mais un ensemble $(x_k,x_{k-1},\dots,x_{k-m_k})$ de précédents itérés pour construire le suivant, par exemple :
$$x_{k+1}=\sum_{i=0}^{m_k}c_i g(x_{k-m_k+i}).$$
Ce procédé d'extrapolation est caractérisé par sa profondeur $m_k$. Alors que ce paramètre est déterminant dans l'efficacité de la méthode, en pratique, la profondeur est fixée sans garantie de convergence de l'algorithme. Dans leurs travaux, les auteurs considèrent deux mécanismes permettant de faire varier de façon adaptative la profondeur $m_k$, à l'étape $k$, au cours des itérations. Une première façon consiste à laisser la profondeur croître jusqu'au rejet de tous les anciens itérés et de redémarrer la méthode. Une autre manière de procéder est d'adapter à chaque étape la profondeur en éliminant les anciens itérés que l'on détecte comme étant moins utiles.
Dans un cadre abstrait et général et sous des hypothèses naturelles, les auteurs ont prouvé la convergence locale et l'accélération de ces deux types de méthodes.
Le comportement de ces algorithmes a été testé pour le calcul numérique de l'état fondamental de molécules en chimie quantique (méthode de Hartree-Fock, modèle de Kohn-Sham). Ces expériences numériques montrent que les variantes avec redémarrage et profondeur adaptative présentent une convergence plus rapide et sont globalement moins coûteuses que la méthode à profondeur fixe, standard dans les codes de chimie quantique.
https://www.esaim-m2an.org/articles/m2an/abs/2021/07/m2an200051/m2an200051.html
Contact : sere@ceremade.dauphine.fr
Instabilité dans les systèmes planétaires

Le "système planétaire" est une approximation newtonienne du système solaire et d'autres systèmes extra-solaires, mise en avant par Poincaré, où les planètes se meuvent autour d'une étoile centrale très massive (le soleil). En première approximation, chaque planète subit la seule attraction du soleil et décrit, comme Newton l'a démontré, une ellipse de Kepler. Mais si l'on prend en compte la petite attraction mutuelle des planètes, le système se dérègle. Pendant un court intervalle de temps à l'échelle astronomique les planètes continuent de se mouvoir le long d'ellipses approchées, mais il est très difficile de prévoir l'effet de la perturbation à long terme.
Le mathématicien Vladimir Arnold a été Professeur au Ceremade de 1993 jusqu'à sa retraite. Parmi ses multiples contributions, il est connu pour avoir exhibé en 1964 un exemple remarquable de système dynamique conservatif presque intégrable avec des courbes intégrales ayant un comportement instable, qui s'apparente à un processus de diffusion. Arnold a conjecturé l'existence de ce phénomène en mécanique céleste mais, depuis 60 ans, la démonstration de l'existence de diffusion dans des systèmes dynamiques même simples s'est avérée très ardue. Andrew Clarke (Universitat Politècnica de Catalunya), Jacques Fejoz (Ceremade) et Marcel Guardia (University of Barcelona) ont récemment démontré l'existence de diffusion d'Arnold dans les systèmes planétaires. Ce travail fait écho à certaines simulations numériques de Jacques Laskar (Observatoire de Paris) et d'autres, qui, depuis une trentaine d'années, montrent l'existence de comportements chaotiques dans le système solaire. Ces simulations sont délicates parce que les erreurs de calcul s'accumulent rapidement, alors que les temps d'intégration sont longs. Le travail mathématique en question montre rigoureusement que certaines planètes peuvent voir leur plan de révolution progressivement se retourner (leur mouvement autour du soleil devenant donc rétrograde) un nombre arbitraire de fois, ou qu'une planète peut voir son ellipse grandir dans une proportion quelconque donnée.
https://www.quantamagazine.org/new-math-shows-when-solar-systems-become-unstable-20230516/
https://arxiv.org/abs/2303.05979
Contact : fejoz@ceremade.dauphine.fr
La tragédie des communs: coopération et compétition pour les pêcheries

Imaginons une mer habitée par des poissons, et supposons que cette mer soit suffisamment hospitalière pour que les poissons y survivent en grand nombre. Peut-on prédire ce qui va se produire si l’on perturbe cet écosystème en y introduisant des pêcheurs ? Quelles conséquences leur pêche aura-t-elle sur la population de poissons ?
Z. Kobeissi (Inria), I. Mazari-Fouquer (Ceremade) et D. Ruiz-Balet (Imperial College London) ont étudié ce problème en mettant en évidence plusieurs phénomènes. D'abord, si les pêcheurs sont en compétition les uns avec les autres, alors leurs actions cumulées peuvent entraîner l’extinction des poissons. Si néanmoins ils coopèrent, non seulement les poissons survivent, mais chaque pêcheur remporte plus, à un niveau individuel, que s’il était en concurrence avec les autres ! Ces résultats, qui offrent une illustration de la "tragédie des commun"s, les a poussés à étudier d’autres modèles pour quantifier de manière plus précise ces effets.

Représentation visuelle de l’extinction de poissons. En bleu, la densité des poissons et, en rouge, la densité des pêcheurs.
Contact : mazari@ceremade.dauphine.fr
Rayon spectral de matrices aléatoires
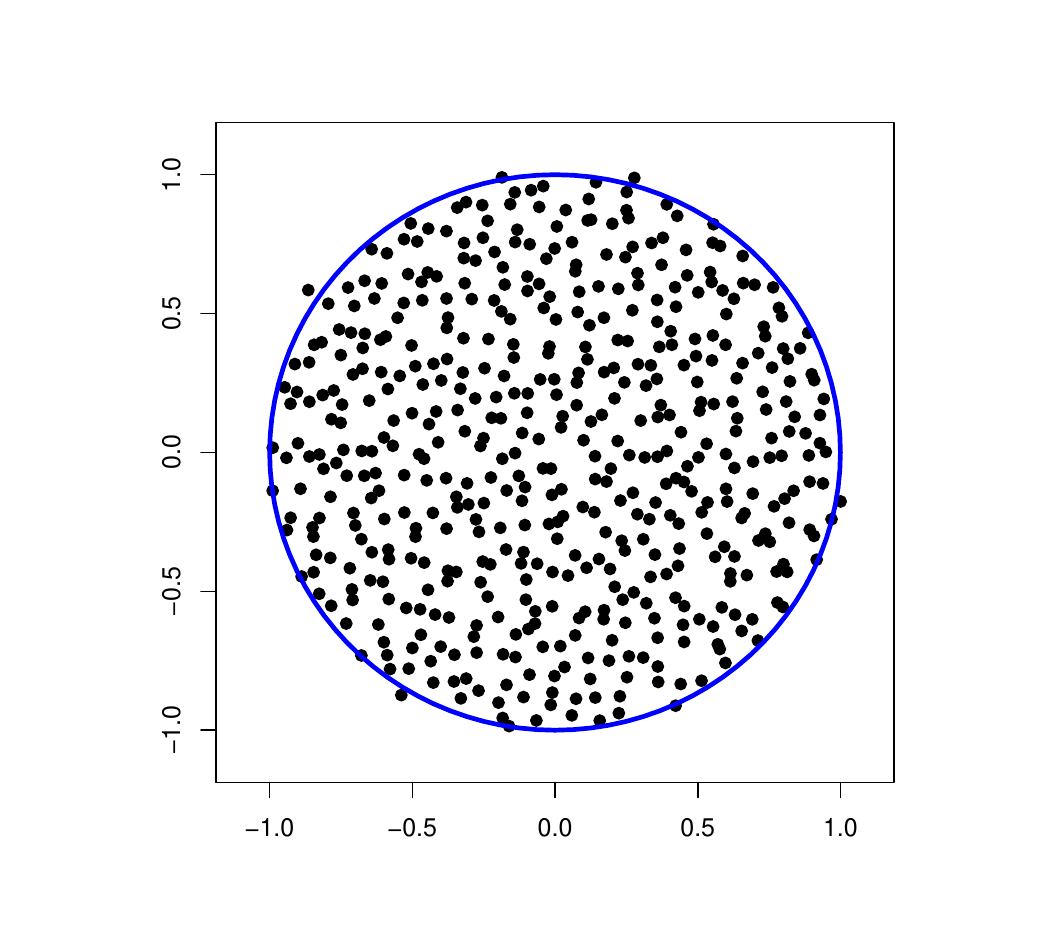
Charles Bordenave (CNRS Aix-Marseille), Djalil Chafaï (Ceremade), et David García-Zelada (Aix-Marseille, ancien doctorant du Ceremade) ont établi dans https://link.springer.com/article/10.1007/s00440-021-01079-9, que pour toute matrice carrée remplie de variables aléatoires indépendantes et équidistribuées, centrées et réduites, le rayon spectral est équivalent à la racine de la dimension. Ce phénomène de grande dimension découle de la convergence du polynôme caractéristique réciproque, sur le disque critique, vers une fonction analytique aléatoire qui ne s'annule pas. Ce résultat optimal précise le phénomène d'uniformisation sur le disque découvert par Jean Ginibre vers 1965 et Vyacheslav L. Girko vers 1980, et et transformé en théorème définitif sous ces hypothèses optimales par Terence Tao et Van Vu vers 2010. Que se passe-t-il quand la variance est infinie ? Un début de réponse substantiel avait été fourni vers 2010 par Charles Bordenave, Pietro Caputo et Djalil Chafaï :
https://link.springer.com/article/10.1007/s00220-011-1331-9
Contact : chafai@ceremade.dauphine.fr
Homogénéisation et jeu de percolation

J.-B. Fermanian (Université Paris-Saclay), W. Feldman (University of Utah) et B. Ziliotto (CEREMADE) ont construit un exemple d'équation de Hamilton-Jacobi stochastique du deuxième ordre qui ne s'homogénéise pas lorsque l'échelle de temps et d'espace devient grande. L'exemple repose sur un jeu où deux adversaires déplacent une balle sur $\mathbb{Z}^2$, en subissant un coût stochastique qui dépend de l'endroit où est la balle. Ce type de jeu peut être vu comme une généralisation du problème de percolation de premier passage au cas de deux joueurs. La figure représente une réalisation de ces coûts, qui sont élevés pour le Joueur 1 dans les zones blanches, et faibles dans les zones noires.
https://www.sciencedirect.com/science/article/pii/S0022039621000164
Contact : ziliotto@ceremade.dauphine.fr
Gender Stereotypes Can Explain the Gender-Equality Paradox
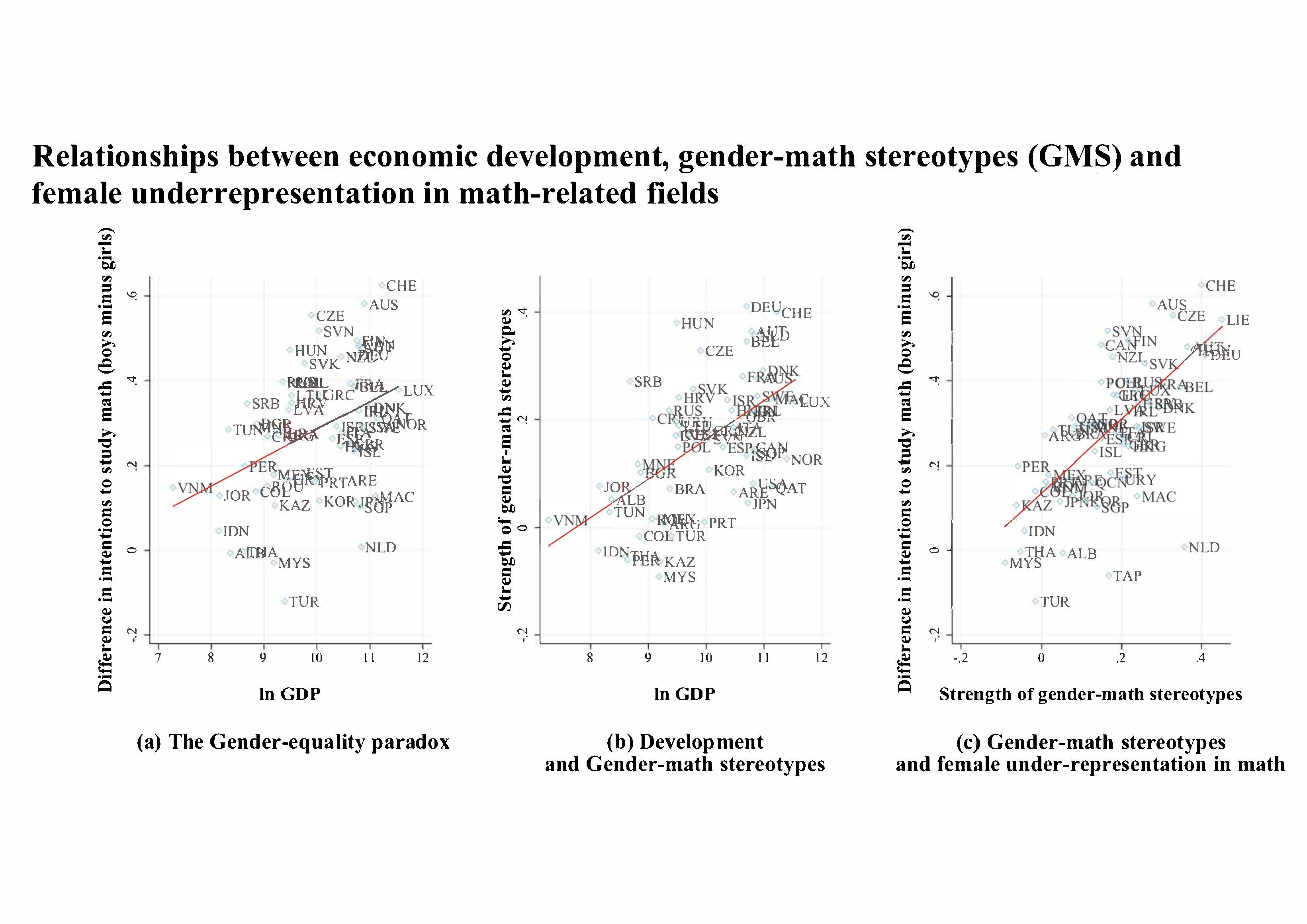
Les femmes sont plus nombreuses que les hommes dans l’enseignement supérieur mais fortement sous-représentées dans les filières qui mobilisent le plus les mathématiques, filières qui mènent, en moyenne, à des emplois mieux rémunérés. Cela représente, de plus, une perte de talents dans des domaines en forte croissance tels que informatique et IA.
Cette sous-représentation est, d'autant plus forte que les pays sont plus développés et plus égalitaires (paradoxe de l’égalité des sexes). Certains auteurs, comme G. Stoet et D. Geary, y voient une preuve de différences d’intérêt innées et intrinsèques entre filles et garçons, qui effectueraient alors des choix d’étude/métiers différents dès qu’on en leur en laisse la liberté. Nous en proposons une autre explication sur la base d'une mesure des stéréotypes associant hommes et mathématiques. Ces stéréotypes apparaissent nettement plus forts dans les pays développés et égalitaires, y compris les pays les plus réputés pour l’égalité entre les sexes comme les pays nordiques. https://theconversation.com/pourquoi-legalite-entre-les-sexes-nefface-t-elle-pas-les-segregations-dans-les-filieres-scientifiques-152272
https://www.pnas.org/content/117/49/31063
Contact : jouini@ceremade.dauphine.fr
Quel est le lien entre un verre de whisky on the rocks et notre laboratoire?

Pourquoi, bien qu'étant solide, le verre a une structure microscopique qui s'apparente beaucoup plus à celle du whisky qu'à celle des glaçons? Comment concilier la structure désordonnée du verre avec les cours de physique qui nous enseignent que lorsqu'un liquide se solidifie une structure cristalline ordonnée apparaît? Ces questions et bien d'autres fascinent et hantent depuis longtemps les physiciens de la matière condensée.
Cristina Toninelli étudie une classe de modèles de particules sur réseaux qui a été introduite par les physiciens dans le but de modéliser la transition liquide/verre, les Kinetically Constrained Models (KCM). Les particules évoluent selon une dynamique stochastiques avec des contraintes locales qui empêchent les mouvements en l'absence d'un nombre suffisant de sites vides dans un voisinage bien choisi, ce qui peut donner lieu à un arrêt de la dynamique à haute densité. Mais... qu'est-ce-que signifie "bien choisi" au juste? En modifiant ce voisinage, le comportement des KCM change drastiquement! Cristina Toninelli s'est attaquée aux variations des échelles de temps des KCM avec les contraintes. Dans une série de travaux en collaboration avec Ivailo Hartarsky (doctorant au Ceremade), Laure Marêché (ancienne doctorante, Strasbourg), Fabio Martinelli (Rome) et Rob Morris (Rio de Janeiro), ils ont identifié les classes d'universalités pour les KCM en dimension 2, et déterminé les échelles de temps du processus stationnaire dans chaque classe. Il en découle un comportement très riche, encore plus que celui des dynamiques (déterministes) de percolation bootstrap auxquels la dynamique stochastique des KCM s'apparente étroitement. Des nombreuses questions restent ouvertes... Que se passe-t-il hors équilibre? Quid du comportement en plus grand dimension?
Contact : toninelli@ceremade.dauphine.fr